Read more
Solution Poisson's Equation In a Rectangular Domain Using 5-Point Stencil
Poisson's equation in a square domain $0 \leq x,y \leq 1$ with source term given by $q(x)=100*\sin(\pi x)*\sin(\pi y)$. The boundaries of the domain are maintained at $u=0$. Determine the solution using finite difference method.
Solution:
Discretizing domain uniformly with step size h and k along x and y direction. Using five point stencil, equation at each node is given by
$$\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{h^{2}}+\frac{u_{i,j+1}-2u{i,j}+u{i,j-1}}{k^{2}}=-q(i,j)$$
$$u_{i,j}=\frac{1}{\frac{2}{h^{2}}+\frac{2}{k^{2}}}(\frac{u_{i+1,j}+u_{i-1,j}}{h^{2}}+\frac{u_{i,j+1}+u{i,j-1}}{k^{2}}+q(i,j))$$
where $q(i,j)=100*\sin(\pi x_{i})*\sin(\pi y_{j})$
Here a MATLAB code is given below. Choosen $m=n=11$ grid to solve the problem using SOR (successive overrelaxation).
Mathematica Code:
- In this algorithm, changing the value of $sor=1$ gives the "Gauss-Seidel iteration", and $sor=0$ gives "Jacobi iteration" and $1< sor < 2$ gives the "successive overrelaxation result(SOR)".
- The successive overrelaxation method generally used for elliptical pdes.











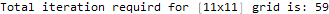



0 Reviews
If you have any doubts, please let me know!